

Lesson 2-4 Graphing Ordered Pairs on a Four Quadrant Coordinate Plane. The angle \(POQ\) is \(30^\circ\) and is called the related angle for \(210^\circ\). 6th Grade Math: integers/coordinate plane No teams 1 team 2 teams 3 teams 4. To find the sine and cosine of \(210^\circ\), we locate the corresponding point \(P\) in the third quadrant. In this quadrant, the sine and cosine ratios are negative and the tangent ratio is positive. We will find the trigonometric ratios for the angle \(210^\circ\), which lies in the third quadrant. A 2-dimensional graph, Cartesian plane, includes negative and positive values of both x and y. The Single Quadrant graph paper has options for one grid per page, two per page, or four per page. The Coordinate Plane Graph Paper may be selected for either single or four quadrants paper. Step 2: Plotting the points and joining with a line we get. We have Standard Graph Paper that can be selected for either 1/10 inch, 1/4 inch, 3/8 inch, 1/2 inch or 1 centimeter scales. Step 1: Given equation 2x y 3 for y 0, x 3/2 for x 2, y 2 2 3 43 1. The method is very similar to that outlined in the previous section for angles in the second quadrant. Graph the line in the quadrant 1, whose equation is given below. If a point lies on the x-axis then its y-coordinate is 0. Furthermore, what quadrant is the point 0 0 in Note that points that lie on an axis do not lie in any quadrant. Quadrants are named using the Roman numerals I, II, III, and IV beginning with the top right quadrant and moving counter clockwise. In the module Further trigonometry (Year 10), we saw that we could relate the sine and cosine of an angle in the second, third or fourth quadrant to that of a related angle in the first quadrant. These four sections are called quadrants. These are summarised in the following diagrams.ĭetailed description of diagram Related angles Angles in the third quadrant, for example, lie between \(180^\circ\) and \(270^\circ\).īy considering the \(x\)- and \(y\)-coordinates of the point \(P\) as it lies in each of the four quadrants, we can identify the sign of each of the trigonometric ratios in a given quadrant. So the question is line l in the xy plane contains points from each of quadrants 2 3 and 4 but no points of quadrant 1 which of the following must be true we have four options these are actually the statements which will fulfill this situation which is there is a line we have a line in the xy plane xy plane and this line is going from quadrants two three and four because the question says it has a point from quadrants 2 3 and 4 so it must be going from these quadrants T3 quadrants 2 3 and 4 but not 5.The coordinate axes divide the plane into four quadrants, labelled first, second, third and fourth as shown. Choice C is incorrect because if a line with a positive slope passes through Quadrant IV, it must pass through Quadrant I as well. We need at least two points or ordered pairs to graph the. Choice B is incorrect because a line with a slope of zero is a horizontal line and, if a horizontal line passes through uadrant II, it must pass through Quadrant I as well. Graphing a line in quadrant 1, We graph a line whose equation is given, say for example y 3x. Choice A is incorrect because a line with an undefined slope is a vertical line, and if a vertical line passes through Quadrant IV, it must pass through Quadrant I as well. Lesson 2-4 Graphing Ordered Pairs on a Four Quadrant Coordinate.
This implies that line l has a negative slope, since between the negative x-intercept and the negative y-intercept the value of x increases (from negative to zero) and the value of y decreases (from zero to negative), so the quotient of the change in y over the change in x, that is, the slope of line l, must be negative. 6th Grade Math: integers/coordinate plane No teams 1 team 2 teams 3 teams 4 teams 5. It is possible for line l to pass through Quadrants II, III, and IV, but not Quadrant I, only if line l has negative x- and y-intercepts.

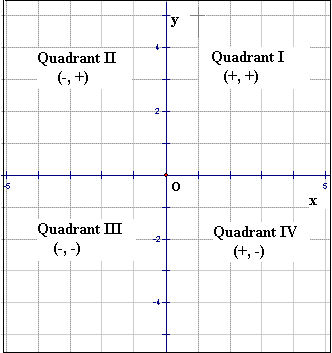
Example: Write the ordered pairs for points A, B, and C shown on the. Solution : The quadrants of the xy-plane are defined as follows: Quadrant I is above the x-axis and to the right of the y-axis, Quadrant II is above the x-axis and to the left of the y-axis, Quadrant III is below the x-axis and to the left of the y-axis, and Quadrant IV is below the x-axis and to the right of the y-axis. Two points, one in quadrant I and one in quadrant III are shown in the figure above.


 0 kommentar(er)
0 kommentar(er)
